Наконец, третий закон Кеплера, уже упоминавшийся ранее, связывает между собой период обращения частицы Т и большую ось эллипса – а. Закон всемирного тяготения Ньютона уточнил эту зависимость, связав ее с массой центрального тела. Уточненный закон можно записать в форме:

или

            Из этого выражения видно, что период обращения однозначно зависит от длины большой оси, возрастая от нуля до бесконечности по мере увеличения орбитального радиуса.

            Константы движения Е и L можно выразить через радиусы перигелия – r₁ и афелия - r₂. В этих точках скорость перпендикулярна радиус–вектору, поэтому sin φ = 1.Формула для L упрощается: L = v₁r₁ = v₂r₂. Решая систему уравнений,

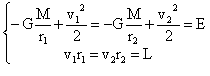
находим выражения для констант. 

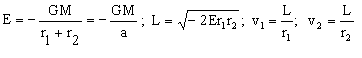
                Заметим, что энергия Е и период обращения Т зависят только от длины большой оси а = r₁  + r₂, т.е. эти величины одинаковы для всех частиц, у которых равны средние радиусы орбит R = .

Для момента импульса L это не так. Его значение при одной и той же длине большой оси тем больше, чем «круглее» орбита, т.е. чем меньше разность радиусов афелия и перигелия r₂ – r₁  и, соответственно, чем меньше эксцентриситет орбиты 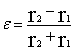. Значение  L максимально для круговой орбиты, для которой r₂ = r₁ = R.

            Все частицы протопланетного диска обращаются вокруг центрального тела в одном и том же направлении, допустим, для определённости – против часовой стрелки. Рассмотрим взаимодействие двух частиц, одна из которых – «круговая», обращается по круговой, а другая «эллиптическая» - по эллиптической орбитам. Рассмотрим частные случаи центральных взаимодействий частиц в точках афелия и перигелия эллиптической орбиты. Так как удельная энергия – E растёт с увеличением среднего орбитального радиуса, то круговая частица, сталкивающаяся с эллиптической в афелии, имеет большую энергию, а следовательно, и скорость чем эллиптическая частица. Независимо от того, упругий удар или неупругий, она подталкивает эллиптическую частицу, увеличивая её энергию. При столкновении в перигелии, наоборот, круговая частица, имеющая меньшую энергию, тормозит эллиптическую, уменьшая её энергию и скорость движения. И в том и в другом случае происходит округление эллиптической орбиты – в первом с увеличением, во втором – с уменьшением её среднего радиуса.